Catenary Cut

Spannt man eine Stoffbahn zwischen zwei Fixpunkten, so wird sie immer etwas durchhängen, egal wie stark man sie spannt. Deshalb werden sich immer entlang der Linie zwischen den Fixpunkten Falten finden. Bei Tarps oder beim Zelten sind diese Falten eigentlich unerwünscht. Sie neigen zum Flattern im Wind und Kondenswasser läuft eventuell nicht mehr ungehindert zum Rand des Tarps ab, außerdem sieht das Zelt im Katalog mit Falten nur halb so schnittig aus wie ohne Falten.

Tarp ohne Catenary Cut

Das oben im sog. diamond pitch aufgebaute Tarp hat entlang der gespannten Diagonalen die o. g. Längsfalten ausgebildet. Diese können durch eine stärkere Stoffspannung zwar minimiert, aber nie komplett eliminiert werden. Die Stoffspannung ist außerdem durch die Bruchlast des Materials und vorher wahrscheinlich durch die Haltekraft der Heringe begrenzt.

Tarp mit Catenary Cut

Um diese Falten zu verhindern und somit eine gleichmäßigere Spannung auf die gesamte Stofffläche zu bringen muß das überschüssige Material weg. Dies erreicht man mit einem sogenannten Catenary Cut (kurz auch catcut genannt). Die Firstnaht im oben fotografierten Tarp ist als ein solcher catcut ausgeführt, die Längsfalten treten dort nicht auf.

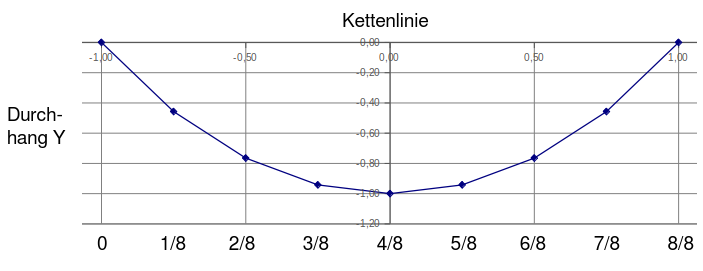
Der Catcut folgt theoretisch einer sogenannten Kettenlinie. Das ist die Kurve die eine an zwei Punkten aufgehänge Kette beschreibt. Eigentlich ist die genaue Form der Kurve egal, solange die Steigung der Kurve vom Fixpunkt bis zur Mitte stetig fällt. Im Prinzip träfe das z. B. auch auf Kreisabschnitte, Parabeln oder eben Kettenlinien zu. In der Praxis, beim Zeltbau, beträgt der Durchhang der Kurve auf 2m nur 2-5 cm. Die genaue Form der Kurve spielt bei diesen flachen Kurven kaum eine Rolle, im Prinzip befinden sich die Unterschiede weit innerhalb der Ungenauigkeit durch den Zuschnitt.

Man kann die genaue Form der Kurve z. B. bestimmen in dem man z. B. eine Schnur mit dem gewünschten Durchhang an der Wand aufhängt, viel einfacher geht es aber IMHO mit ein Paar Koordinatenpunkten.